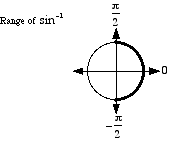|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Inverse Sine The inverse function of sine. Basic idea: To find sin-1(½),
we ask "what
angle has sine equal to ½?" The
answer is 30°. As a result we say More: There are actually many angles that have
sine equal to ½.
We are really asking "what is the simplest, most basic angle that has
sine equal to ½?" As before,
the answer is 30°. Thus Details: What is sin-1(–½)?
Do we choose 210°, –30°, 330° ,
or some other angle? The answer is –30°.
With inverse sine, we select the angle on the right half of the unit
circle having measure as close to zero as possible. Thus In
other words, the range of Note: arcsin refers to "arc sine", or the radian measure of the arc on a circle corresponding to a given value of sine. Technical note: Since none of the six trig functions sine,
cosine, tangent, cosecant, secant, and cotangent are one-to-one, their inverses are not functions. Each trig function can have its
domain restricted, however, in order to make its inverse a function.
Some mathematicians write these restricted trig functions and their
inverses with an initial capital letter (e.g. Sin or
See also Inverse trigonometry, inverse trig functions, interval notation
|
| this page updated
15-jul-23
Mathwords: Terms and Formulas from Algebra I to Calculus written, illustrated, and webmastered by Bruce Simmons Copyright © 2000 by Bruce Simmons All rights reserved |
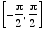 .
.