For the following, assume that x, y, a, and b are all positive. Also assume that a ≠ 1, b ≠ 1.

Definitions

1. log_a x = N means that a^N = x.

2. log x means log₁₀ x. All log_a rules apply for log. When a logarithm is written without a base it means common logarithm.

3. ln x means log_e x, where e is about 2.718. All log_a rules apply for ln. When a logarithm is written "ln" it means natural logarithm.
    Note: ln x is sometimes written Ln x or LN x.

Rules

1. Inverse properties:   log_a a^x = x   and   a^(loga ^x) = x

2. Product:  log_a (xy) = log_a x + log_a y

3. Quotient: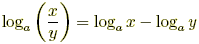  

4. Power:   log_a (x^p) = p log_a x

5. Change of base formula:

Careful!!

log_a (x + y) ≠ log_a x + log_a y

log_a (x – y) ≠ log_a x – log_a y