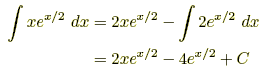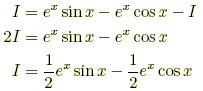|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Integration by Parts A formula used to integrate the product of two functions.
See also
|
| this page updated
15-jul-23
Mathwords: Terms and Formulas from Algebra I to Calculus written, illustrated, and webmastered by Bruce Simmons Copyright © 2000 by Bruce Simmons All rights reserved |